By: Hilary Weller


Atmospheric convection – the dynamics behind clouds and precipitation – is one of the biggest challenges of weather and climate modelling. Convection is the driver of atmospheric circulation, but most clouds are smaller than the grid size and so cannot be represented accurately or at all. Consequently, all but the highest resolution models use convection parameterisations – statistical representations which estimate the heat and moisture that would be produced and transported by clouds if they were resolved. These parameterisations have become sophisticated, estimating the mass that is transported upwards and how this will influence the momentum, temperature, moisture and precipitation. Without these parameterisations climate models dramatically fail. However, there are still big problems with these parameterisations; they tend to produce unrealistic hot columns of air and the main regions of convection in the tropics are usually misplaced (see Figure 1). These are large heat sources for the global atmosphere and so errors in these locations have knock-on effects across the globe.
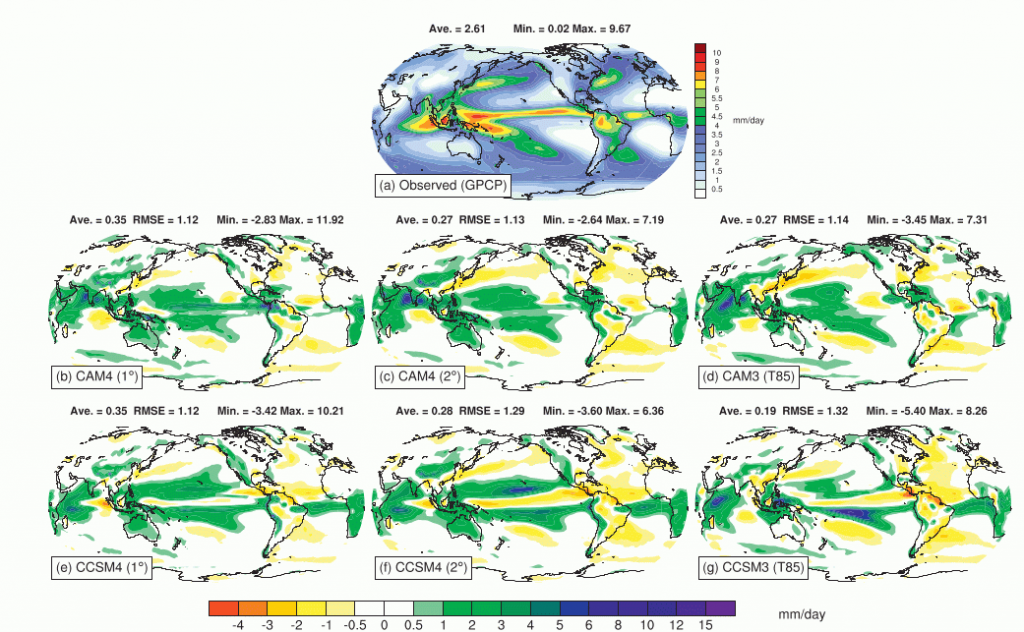
Figure 1: Fig 11 from Neale et al, (2013) showing “Annually averaged (a) observed precipitation from GPCP (1979–2003) and model precipitation biases (mm day 21 ) in AMIP-type experiments for (b) CAM4 at 18, (c) CAM4 at 28, and (d) CAM3 at T85, and in fully coupled experiments for (e) CCSM4 at 18, (f) CCSM4 at 28, and (g) CCSM3 at T85.”
There are two assumptions made in convection parameterisations that could be to blame for their poor performance. Firstly, there is no memory of the properties of convection from one time-step to the next. The convection properties are calculated each time step from scratch as if there had been no convection in the previous time step. Secondly, although there is a class of convection scheme called “mass flux”, convection schemes do not actually transport air upwards. They transport the heat, moisture and momentum but the distribution of mass in the vertical is not changed by the convection scheme. Removing these assumptions is quite tricky. You realise that what you need to do is solve the same equations of motion in clouds and outside clouds, but these need to be modelled separately because the clouds are such a small fraction of the total volume. This is the multi-fluid approach. Separate equations for velocity, temperature, moisture, and volume fraction are solved for the air in clouds and the environmental air, outside clouds. As the clouds and the environment are interwoven, we assume that they share the same pressure.
John Thuburn and I are working on making this approach work as part of the NERC/Met Office Paracon project to develop big changes to the way that convection is parameterised in order to remove some of the less realistic assumptions (Thuburn et al, 2018, Weller and McIntyre, 2019). As ever, it is proving more difficult than we expected. We knew that we would need to solve simultaneous equations for the properties in and outside the clouds and that these would need to be simultaneous with the single pressure. I naively thought that this would be sufficient and that my expertise in this area would make it possible whereas convection modellers are usually less familiar with this simultaneous solution procedure. However, it turns out that the multi-fluid equations can be unstable. They are easy to stabilise but the stabilisation can have the effect of making the two fluids behave as one which defeats the purpose. We need to make the two fluids move through each other. John has made some good progress on this (Thuburn et al, 2019).
The multi-fluid equations need transfer terms to transfer air in and out of the clouds. These are not a mystery. Traditional parameterisations predict these transfers, and these have been thoroughly validated and tested. However, the multi-fluid equations are sensitive to these transfer terms and do not behave in the same way as the traditional parameterisations. We also want to base the transfers on the sub-grid scale variability both inside and outside the cloud so that a cloud is formed if some of the air in a grid box is ready to rise and condense out water. There is plenty to do.
While the multi-fluids team from the Paracon project have been working on simultaneous solutions of equations for in and outside clouds, ECMWF thought that they would try a more direct approach – simply adding a term to the continuity equation based on the mass flux predicted by their traditional parameterisation (Malardel and Bechtold, 2019). This was also the approach taken by Kuell and Bott (2008). The problem with this approach is that it will be unstable if a large fraction of a grid box is cloudy. However, ECMWF and Kuell and Bott (2008) have not reported any stability problems, although the ECMWF approach did ensure that only a small fraction of each grid box is transported by the convection scheme. The results so far seem promising. However, to be able to increase the resolution and run with sufficiently long time steps so that the model is competitive, we will need the multi-fluid approach.
References:
