By Dr. Joanne Waller  (University of Reading) 10th September 2014

The forecasting of intense rainfall requires a best guess of the current atmospheric state; this is calculated using a data assimilation scheme. Data assimilation techniques combine observations with a model prediction of the state, known as the background, to provide a best estimate of the state, known as the analysis.

For a data assimilation scheme to produce an optimal estimate of the state the errors associated with the observations and the background must be well understood and correctly specified. Previously much attention has been given to the errors associated with the background and a sophisticated representation of these errors is now used in the assimilation. In contrast, less emphasis has been given to understanding the nature of the observation errors.

The errors associated with the observations can be attributed to four main sources:

• Instrument error.
• Error introduced in the observation operator  (a model that allows the predicted quantity to be compared to the observation, for more information see this blog).
• Errors of representativity – these arise where the observations can resolve spatial scales that the model cannot.
• Pre-processing errors  – errors introduced by pre-processing of the data

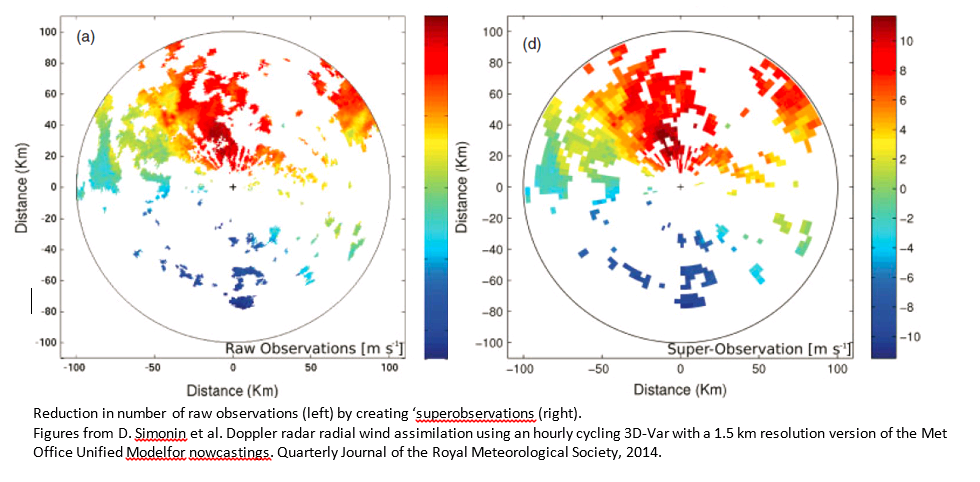
For most observations the instrument error is uncorrelated; the remaining sources of error are likely to introduce correlations which are both state and time dependent.  Typically these correlations are not well understood and have been ignored in operational assimilation. Instead, the unknown and unaccounted for correlations are represented by inflating the error variance.  The quantity of observations used is also reduced, hence reducing the error correlations, either by discarding data or combining data to create superobservations. To improve the use and quantity of observations used in the data assimilation scheme it is imperative to understand and accurately represent the errors associated with the observations.

As part of project FRANC we are aiming to estimate and incorporate into the assimilation correlated error statistics for a number of observation types. Information on the errors associated with the observation is hidden in the ‘innovation’, which is the difference between the value of the measured observation and the corresponding model equivalent; this may be taken from either the background or analysis. To extract these observation errors, we use a diagnostic that calculates statistical averages of background and analysis innovations to provide an estimate of the observation error covariance matrix. In theory this method provides an exact estimate of the observation errors. However, in complex operational systems many simplifying assumptions are made and therefore the result of the diagnostic may not be exact, though it is expected to be a reasonable approximation.

Our studies have attempted to calculate and understand the errors associated with Doppler radar radial wind measurements.  Using the diagnostic we calculated observation error correlations along the radar beam at different ranges away from the radar and at different heights in the atmosphere. Initial results show that Doppler radar radial wind error variances increase with height. Results also show that correlation length scales range between 10km and 40km and are longer at lower heights and at far range. Now we have some idea of the observation error statistics associated with Doppler radar radial winds we must attempt to include them in the assimilation (a challenge in itself!). The correct inclusion of these errors in the assimilation should improve the analysis, which in turn should improve the forecasts of intense rainfall.