By Eunice Lo
Sulphate aerosol injection (SAI) is one of the geoengineering proposals that aim to reduce future surface temperature rise in case ambitious carbon dioxide mitigation targets cannot be met. Climate model simulations suggest that by injecting 5 Tg of sulphur dioxide gas (SO2) to the stratosphere every year, global surface cooling would be observed within a few years of implementation. However, temperature fluctuations occur naturally in the climate system too. How could we detect the cooling signal of SAI amidst internal climate variability and temperature changes driven by other external forcings?
The answer to this is optimal fingerprinting (Allen and Stott, 2003), a technique which has been extensively used to detect and attribute climate warming to human activities. Assuming a scenario (G4, Kravitz et al., 2011) in which 5 Tg yr-1 of SO2 is injected to the stratosphere on top of a mid-range warming scenario called RCP4.5 from 2020-2070, we first estimate the climate system’s internal variability and the temperature ‘fingerprints’ of the geoengineering aerosols and greenhouse gases separately, and then compare observations to these fingerprints using total least squares regression. Since there are no real-world observations of geoengineering, we cross-compare simulations from different climate models. This gives us 44 comparisons in total, and the number of years that would be needed robustly to detect the cooling signal of SAI in global-mean near-surface air temperature is estimated for each of them.
Figure 1(upper) shows the distribution of the estimated time horizon over which the SAI cooling signal would be detected at the 10% significance level in these 44 comparisons. In 29 of them, the cooling signal would be detected during the first 10 years of SAI implementation. This means we would not only be able to separate the cooling effect of SAI from the climate system’s internal variability and temperature changes driven by greenhouse gases, but we would be able to achieve this early into SAI deployment.
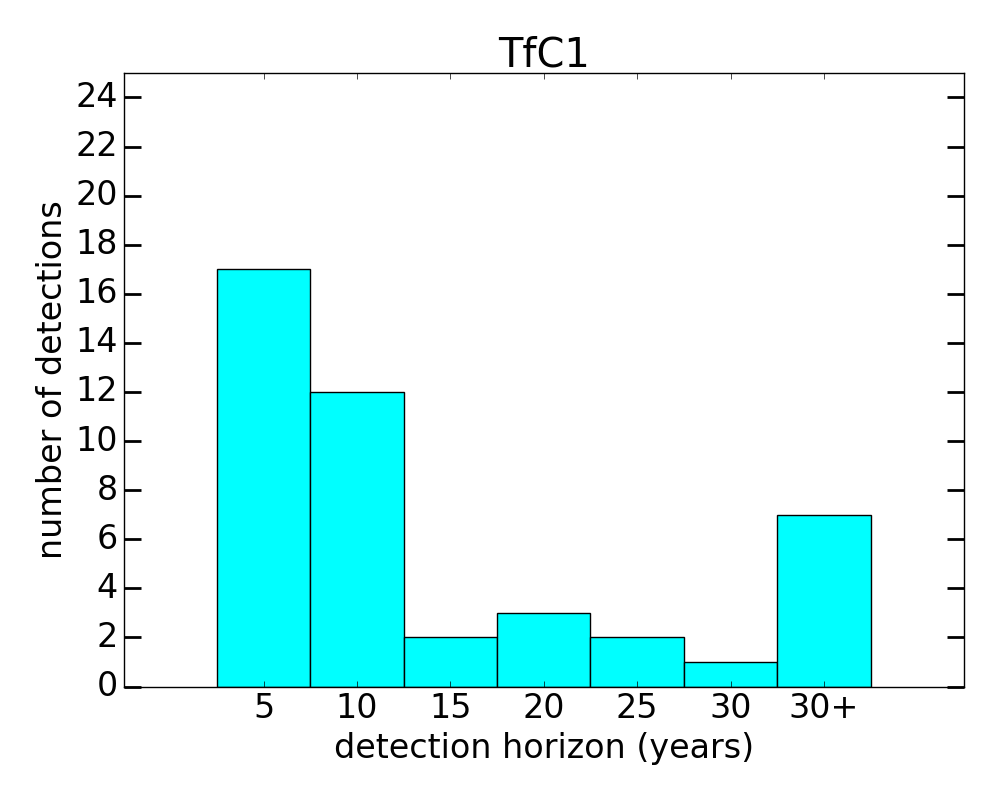

Figure 1: Distribution of the estimated detection horizons for the SAI fingerprint using (upper graph) the conventional bi-variate method and (lower graph) the non-stationary detection method.
The above results are tested by applying a variant of optimal fingerprinting to the same problem. This new method assumes a non-stationary background climate that is mainly forced by greenhouse gases, and attempts to detect the cooling effect of SAI against the warming background using regression (Bürger and Cubasch, 2015). Figure 1(b) shows the distribution of the detection horizons estimated by using the new method in the same 44 comparisons: 35 comparisons would require 10 years or fewer for the cooling signal to be robustly detected. This shows a slight improvement from the results found with the conventional method, but the two distributions are very similar.
To conclude, we would be able to separate and thus detect the cooling signal of sulphate aerosol geoengineering from internal climate variability and greenhouse gas driven warming in global-mean temperature within 10 years of SAI deployment in a future 5 Tg yr-1 SAI scenario. This could be achieved with either the conventional optimal fingerprinting method or a new, non-stationary detection method, provided that the climate data are adequately filtered. Research on the effects of different data filtering techniques on geoengineering detectability is not included in this blog post, please refer to the article cited at the top for more details.
NOTE: How feasible is the injection of 5 Tg yr-1 SAI scenario? Robock et al. (2009) estimated the cost of lofting 1 Tg yr-1 of SO2 into the stratosphere with existing aircraft to be several billion U.S. dollars per year. Scaling this to 5 Tg yr-1 is still not a lot compared to the gross world product. There are practical issues to be addressed even if existing aircraft were to be used for SAI, but the deciding factor of whether to implement sulphate aerosol geoengineering or not should be its potential benefits and side effects, both on the climate system and the society.
REFERENCES
Allen, M. R., and P. A. Stott, 2003. Estimating signal amplitudes in optimal fingerprinting, Part I: Theory. Climate Dynamics, 21.5-6: 477-491.
Bürger, Gerd, and Ulrich Cubasch, 2015. The detectability of climate engineering. Journal of Geophysical Research: Atmospheres, 120.22.
Kravitz, Ben, et al., 2011. The geoengineering model intercomparison project (GeoMIP). Atmospheric Science Letters 12.2: 162-167.
Robock, Alan, et al., 2009. Benefits, risks, and costs of stratospheric geoengineering. Geophysical Research Letters 36.19.
