There is a striking resemblance between some waves generated in the atmosphere in flow over isolated mountains and wave patterns in the wakes of ships, boats, or even ducks swimming in a pond. Typically, these waves are delimited by a triangular wake with a well-defined angle (of about 39 degrees) opening downstream of the obstacle that generates them (see Figures 1, 2 and 3). The shape of this wake was first determined theoretically by Lord Kelvin in his pioneering study of ship waves (Thomson, 1887). Ship waves and “duck waves” are forced via direct piercing of the air-water interface by the body that acts as a wave source.

Figure 1: Waves in a cloud layer generated in flow over the South Sandwich islands (source: https://www.atmos.washington.edu/2010Q1/536/figs/mtn_waves/SouthSandwich_shipwaves.jpg)

OLYMPUS DIGITAL CAMERA
Figure 2: Waves produced in the wake of a boat in a river (source: http://www.wikiwaves.org/File:Wake.avon.gorge.arp.750pix.jpg)

Figure 3: Waves generated by a swimming duck (source: https://www.itp.uni-hannover.de/~zawischa/ITP/strange.html)
In flow over mountains, the source obstacle typically does not touch the deformed interface. Rather, waves are generated remotely, in the same way as surface distortions in a stream are caused by stones at its bottom. Additionally the density gradient where the waves propagate is not as sharp as an air-water interface, typically corresponding to a temperature inversion (Teixeira et al., 2013). Nevertheless, all of these waves can be approximated as interfacial waves where gravity is the restoring force, and the angle, as well as the spatial structure, of the wake, can be explained using linear surface gravity wave theory (e.g. Lighthill, 1978, chapter 3). The resistance force produced by these waves influences the design and powering characteristics of ships, and has gravity wave drag as its atmospheric counterpart.
Typically, the waves depicted in Figures 1-3 are “deep-water waves”, with the wavelength not exceeding the fluid depth. This means that they are dispersive, and their group speed (at which energy is transported) is half the phase speed (at which individual crests and troughs travel). Waves within a wake are stationary with respect to their source, so they must propagate at an angle such that the projection of the mean fluid speed matches their phase speed. Therefore, they cannot be faster than the flow. The interface is only appreciably deformed in the region (defining the wake) where the energy of waves emitted at a given point (and propagating with the group speed) has travelled a distance half that of the crests that are able to keep up with the source (red dots in Figure 4).
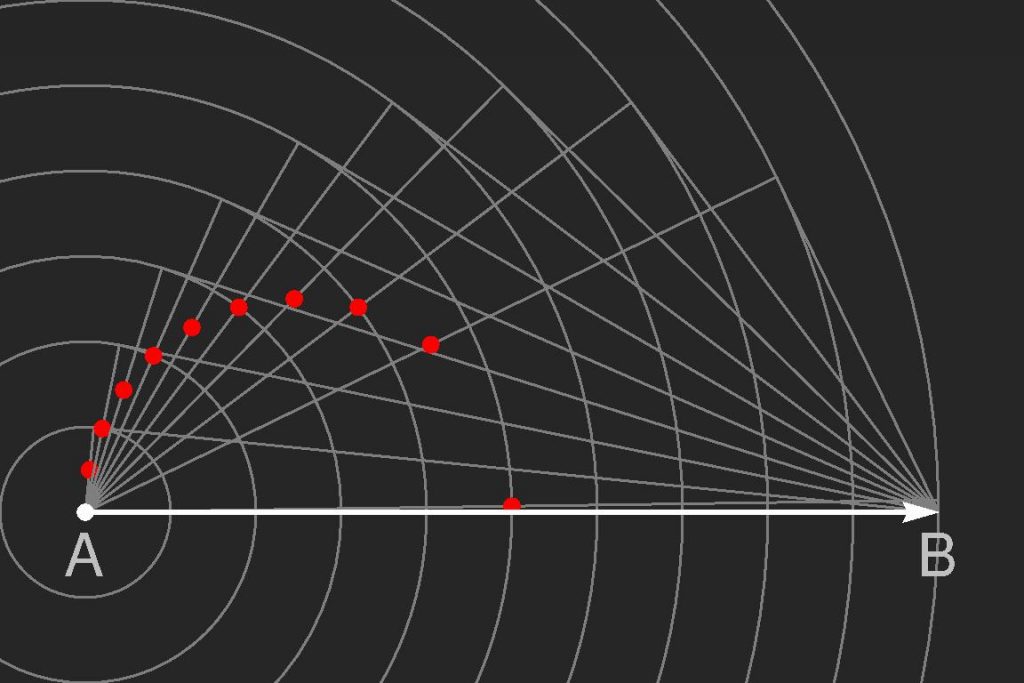
Figure 4: Schematic diagram explaining the angle of Kelvin’s ship wake (source: https://www.itp.uni-hannover.de/~zawischa/ITP/KWake.html)
No wave energy can propagate upstream of a line joining point B in Figure 4 (where the source is located) to a point where this line is tangent to the circle defined by the red dots. The angle between this line and the direction of motion is half the Kelvin ship wake angle, arcsin(1/3) ~ 19.5º. This result only relies on the facts that the wave pattern is stationary and the group speed of the waves is half their phase speed, hence its general applicability to waves that are apparently so different. A distinct speed ratio would produce a different wake angle.
The wave crests near the middle of the wake are perpendicular to the flow and called transverse waves, while those at the edge of the wake make a smaller angle with the flow direction and are known as divergent waves. The latter are shorter than the former (see Figures 2 and 3), since they are geometrically constrained to have a lower phase speed, and the dispersion relation of deep-water gravity waves prescribes that shorter waves propagate more slowly than longer ones.
References
Lighthill, M. J., 1978. Waves in Fluids, Cambridge University Press, 504 pp.
Teixeira, M.A.C., Argain, J.L. and Miranda, P.M.A., 2013. Orographic drag associated with lee waves trapped at an inversion. Journal of the Atmospheric Sciences, 70, 2930-2947. Centaur listing
Thomson, W., 1887. On ship waves. Proceedings of the Institution of Mechanical Engineers, 38, 409-434.
