Sea level rise due to global warming is an important societal issue. This motivated me a few years ago to make it part of my “Introduction to Oceanography’’ module. The main effects are easy to understand. Global sea level mostly changes as the result of adding mass to it, due to melting of land ice sheets, or as the result of expansion caused by warming. One “known fact” that I had been teaching, and thought to understand well, is that sea level does not increase when floating ice melts. Sea level rise only occurs when land ice sheet falls into the ocean, not when it subsequently melts. I was shocked, therefore, to learn at a recent conference on satellite altimetry that I was wrong. One of the talks pointed out a paper by Noerdlinger and Brower (2007), arguing that contrary to popular belief, the melting of floating ice actually increases sea level! The effect had apparently been completely missed by the experts who wrote the sea level chapter in the 4th IPCC assessment report, and only recently included in the 5th IPCC assessment report.
This was quite vexing. Surely, sea level physics is not particle physics, how could have experts been ignorant of basic physics for so long?
 SHUTTERSTOCK 239618599
SHUTTERSTOCK 239618599
As it turns out, the effect had been missed because of a misapplication of Archimedes principle. Archimedes is the famous Greek scientist who is mostly remembered for coming out of his bath shouting ‘Eureka’ (“I discovered it”) upon discovering the principle that bears his name. This principle states that if a body is plunged into a liquid or gas, it will feel a force that is equal to the weight of the fluid displaced.
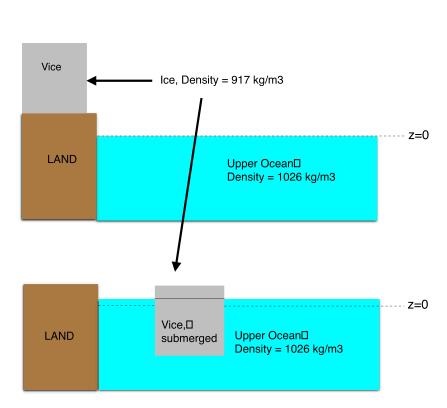
Figure 1. Schematics of an ice sheet initially on land ending up in the ocean as an iceberg or ‘floating ice’. Because ice is much less dense than seawater, part of it remains out of the water, and only the submerged part contributes to increasing sea level. All the volume of the iceberg contributes to sea level, however, once melted, explaining why the melting of floating ice can further contribute to increasing sea level.
This principle is quite powerful, and allows one to easily predict the emerged fraction of an iceberg (the tip of the iceberg). In order for the iceberg to stay in place (to be in equilibrium), its weight must be opposed by the Archimedes force (Figure 1). If Vice, ρice, and mice=Vice ρice denote the volume, density and mass of the iceberg, its weight is miceg, where g is the acceleration of gravity. The Archimedes force, on the other hand, is equal to the weight of the seawater displaced, that is Vice-submerged ρseawater g, where ρseawater is the density of seawater, and Vice-submerged is the submerged volume of the iceberg. This implies that
Vice-submerged = (ρice /ρseawater)Vice
This formula explains that the tip of an iceberg owes its existence to ice having a much lower density than seawater. As to the sea level increase Δhice due to dumping the iceberg into the sea, it is due to the volume displaced Vice-submerged, not the total volume Vice. This volume is equal to Δhice times the total area of the ocean Aocean,leading to
Δhice= Vice-submerged / Aocean = (ρice/ρseawater)Vice/Aocean
In contrast, the sea level increase Δhmelt due to the melted iceberg will be due to the total mass of the iceberg. If ρfreshwater denotes the density of freshwater, one will have the equalities mice=Vice ρice =Vfresh ρfreshwater =ρfreshwater Δhmelt Aocean, which yields the result
Δhmelt=(ρice/ρfreshwater)Vice/Aocean
which is different from Δhice. One verifies that the difference is given by
Δhmelt – Δhice = (ρseawater-ρfreshwater)Δhice/ρfreshwater
This formula shows that the difference arises because the density of freshwater is lower than that of salty seawater.
How big is the effect? Typical representative values for the densities of ice, freshwater and seawater are ρice=917 kg/m3, ρfreshwater=1000 kg/m3 and ρseawater=1026 kg/m3, which yields (ρseawater – ρfreshwater)/ρfreshwater=0.026. It means that if an ice sheet dumped into the ocean increases the sea level by 1 metre, its subsequent melting will further increase it by 2.6 centimetres. This is a small effect, but one that needs to be included in discussions of error bars.
In reality, the effect might be somewhat more complex. Indeed, Jenkins and Holland (2007) argue that melting floating ice requires energy, which must come primarily from the ocean. In the same way that warming causes sea level rise due to expansion, cooling will cause a sea level decrease due to contraction, which may largely negate the effect of melting. Modelling this effect is significantly more complex, however, and beyond the scope of this blog.
Whoever said that the physics of sea level change was simple?
REFERENCES
Jenkins A. and D. Holland, 2007. Melting of floating ice and sea level rise. Geophys. Res. Lett, 34, L16609, doi:10.1029/2007GL030784
Noerdlinger, P. D. and K. R. Brower, 2007. The melting of floating ice raises the ocean level. Geophys. J. Int., 170, 145-150.