It might be thought that turbulence is essentially the same everywhere. However, its mixing efficiency depends not only on its intensity (as might be expected intuitively), but also on more subtle properties, such as its anisotropy (which components of the velocity fluctuations are dominant). These characteristics are determined by the mechanisms that generate the turbulence. For example, it is known that convective turbulence (generated by positive heat fluxes into the atmosphere or negative heat fluxes out of the ocean) typically mixes more efficiently than shear-generated turbulence induced by the no-slip boundary condition at the ground. This is not only because heating is often a more potent source of energy than wind shear, but also because convective turbulence is dominated by its vertical velocity fluctuations (which have a greater mixing ability – in the vertical), whereas shear turbulence is dominated by horizontal velocity fluctuations.
Even ignoring thermal effects, turbulence in the oceanic boundary layer has a totally different character from that of atmospheric boundary layer turbulence, because of the different boundary conditions at the air-water interface relative to those at the ground. While, in the atmosphere over flat terrain (undulating terrain is different), the no-slip boundary condition generates shear-driven turbulence, in the oceanic boundary layer, a sheared water current exists near the surface, forced by the wind stress, but it is not the most important aspect. The wind stress also generates surface waves, which have an associated Lagrangian transport in the direction of wave propagation, named “Stokes drift”. This element totally changes the character of the turbulence.
Figure 1 shows foam alignments at the surface of a body of water. This foam, which was probably produced by micro-breaking or white-capping of the surface waves (also caused by the wind), is aligned perpendicularly to the crests of the waves (at least far from the shore) and is also roughly aligned with the wind. This happens because of the presence of coherent vortices (known as Langmuir circulations) in the water, with their axes aligned with both the wind and wave propagation direction. The foam collects at the convergence zones of these vortices at the air-water interface.

Figure 1: Windrows, or foam alignments at the air-water interface of a body of water, induced by the joint effects of a surface current induced by the wind and surface waves via Langmuir Circulations.
Although Langmuir circulations were initially studied as single-scale features, using modal growth linear theories (Craik and Leibovich, 1976), it has become clear that they have multiple scales, so they can be viewed as a separate type of turbulence (named Langmuir turbulence) (McWilliams et al., 1997), distinct from the shear-driven turbulence more common in non-convective boundary layers. The general configuration of Langmuir turbulence is described in Figure 2. The streamwise vortices that dominate Langmuir turbulence are typically aligned with the direction of propagation of surface waves, and within 5˚ to 15˚ of the wind direction. They are characterized by convergence zones (in blue) where foam (or floating debris) collects, vertical velocities of ~5 u*, where u* is the friction velocity in the water, and surface jets at the convergence zones in the direction of both the wind and waves, with velocity perturbations of ~10 – 15 u*. The upwelling/surface-divergence zones of Langmuir vortices are privileged locations for the emergence of plankton.

Figure 2: Schematic diagram showing the configuration of Langmuir turbulence vortices and the associated physical phenomena (from Smith, 2001).
The mechanisms underlying the structure of Langmuir turbulence, and its differences from shear turbulence, are explained in Figure 3. On the left panel, we can see how vertical vorticity (which always exists in turbulence) is tilted and stretched by the vertical profile of the Stokes drift associated with surface waves propagating from left to right. This Lagrangian transport has a maximum at the surface and decays to zero as depth increases. This causes a tilting of the vertical vorticity into the direction of the Stokes drift (which coincides with the direction of wave propagation), and stretching of this vorticity. We will call the wave propagation direction, which typically coincides with the direction of the wind stress and of the shear in the current induced by the wind, the streamwise direction. Stretching of the streamwise vorticity causes its amplification, making this vorticity become dominant in the turbulence. This explains the existence of coherent streamwise vortices in Langmuir turbulence. These vortices are dominated by velocity fluctuations in the spanwise and vertical directions, the latter strongly promoting vertical mixing.
On the right panel of Figure 3, we see how shear-driven turbulence differs from Langmuir turbulence in this respect. Vertical vorticity in the turbulence is equally tilted and stretched into the streamwise direction, now by mean shear in the wind-driven current. But the mean vorticity in the current is also tilted by the circulation induced by the turbulent vorticity, and this causes a partial cancellation of the latter. This is why shear-driven turbulence is not dominated by streamwise vortices, like Langmuir turbulence. Rather, velocity fluctuations in the streamwise direction (sometimes called “streaky structures”) are dominant.


Figure 3: Left: tilting and stretching of vertical vorticity into streamwise vorticity by the Stokes drift of surface waves; Right: tilting and stretching of vorticity in a shear flow (from Teixeira and Belcher, 2002).
The consequences of these differences for the transport of buoyant tracers trapped at the air-water interface are explained in Figure 4 (where a surface wave is assumed to propagate from left to right and/or a wind is assumed to blow from left to right). In wave-driven (or Langmuir) turbulence (diagram on the left), the flow is dominated by streamwise vortices, which at the surface induce primarily spanwise velocity fluctuations (arrows). The convergence zones of this velocity field lead to the concentration of buoyant tracers along lines aligned in the streamwise direction. In shear-driven turbulence (diagram on the right), there is also a tendency for buoyant surface tracers to align in the streamwise direction, but the mechanism that causes it is weaker. This is associated with the confluence that necessarily occurs at the entrance regions to maxima in the dominant streamwise velocity fluctuations (streaky structures).
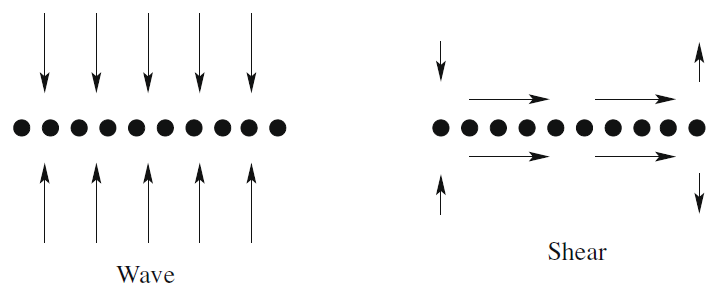
Figure 4: Schematic diagrams showing the transport of buoyant tracers by (Left) streamwise vortices in Langmuir turbulence; (Right) streaky structures in shear-driven turbulence (from Teixeira and Belcher, 2010).
An up-to-date overview of Langmuir turbulence, including motivation of its importance, recent developments in theory, measurements and numerical modelling, and various applications, is provided in a recent short review by the author of this post , published in the latest edition of the Encyclopedia of Ocean Sciences (Teixeira, 2019).
References
Craik, A. D. D., and Leibovich, S. (1976) A rational model for Langmuir circulations. J. Fluid Mech., 73, 401-426. doi: https://doi.org/10.1017/S0022112076001420
McWilliams, J. C., Sullivan, P. P. and Moeng, C.-H. (1997) Langmuir turbulence in the ocean. J. Fluid Mech., 334, 1-30. doi: https://doi.org/10.1017/S0022112096004375
Smith, J. A. (2001) Observations and theories of Langmuir circulation: a story of mixing. In Fluid Dynamics and the Environment: Dynamical Approaches, Lecture Notes in Physics, vol. 566, 295-314, Ed.: Lumley, J.L., Springer. doi: https://doi.org/10.1007/3-540-44512-9_16
Teixeira, M. A. C. (2019) Langmuir circulation and instability. In Encyclopedia of Ocean Sciences (Third Edition), Eds. J. K. Cochran, H. J. Bokuniewicz, P. L. Yager, Academic Press, pp. 92-106. doi: https://doi.org/10.1016/B978-0-12-409548-9.04176-2
Teixeira, M. A. C. and Belcher, S. E. (2002) On the distortion of turbulence by a progressive surface wave. J. Fluid Mech., 458, 229-267. doi: https://doi.org/10.1017/S0022112002007838
Teixeira, M. A. C. and Belcher, S. E. (2010) On the structure of Langmuir turbulence. Ocean Modelling, 31, 105-119. doi: https://doi.org/10.1016/j.ocemod.2009.10.007
