How to analyse your forecast diary properly

By: Jochen Broecker

As you are reading a science blog, I am sure you are interested in science, and either as a parent or during your childhood you will have seen these books aimed at children interested in the natural world. I’m thinking of colourful books with busy layouts and named along the lines of “100 Science Experiments For Little Explorers”, “365 Activities For Young Scientists” or “50 Cool Experiments For Rainy Days”.

A staple of these books is suggesting to start a weather diary as an activity. Depending on the targeted age groups, these might simply involve putting dashes next to a smily sun or a bubbly rain cloud, or be more challenging by asking to record more details and even write little reports.

Suggestions as to what to do with these records are much harder to find. This article suggests to make your weather diary even more interesting by recording not only what has actually happened but also what weather centres (such as the MetOffice) predicted to happen. Further, we will discuss how to do something useful with your records, namely subject them to a proper statistical analysis, thereby checking the quality of the forecasts in some sense.

The challenge is that your forecast diary will most likely not be amenable to the standard statistical tools that are taught in those moderately popular statistics courses for natural scientists. The data instances in your forecast diary will not be temporally independent, which renders the whole analysis a lot more interesting.

The forecast diary

The diary we have in mind records not only the actual event (say “rain” or “no rain” today) but also the corresponding forecast from some weather centre of your choice, let’s say the Met Office. Rain is interesting because the Met Office issues probability of precipitation, or PoP forecasts. These represent the propability of seeing rain during a specific time interval (at a given location). The Met Office uses hourly intervals, but presumably you don’t want to enter records into your diary with such high frequency. As an alternative, you can consult the Dutch or the US Weather Service as they provide daily PoP’s but only for their respective countries. But at least the latter seems to be taking the maximum of the hourly PoP’s as a daily PoP (whatever the theoretical justification). This is something you could apply to the Met Office hourly PoP’s to get daily PoP’s for the UK.

The forecast is expressed in percent, rounded to the nearest multiple of ten. In fact, there are several forecasts available that apply to any given event, namely forecasts with different horizon, also called lead time. You may record forecasts for several lead times in your diary, a typical page of which might look like this:

Forecast Diary
Date	Rain
01.01.20	Yes	20	10	10
02.01.20	No	10	10	10
03.01.20	No	10	0	5
04.01.20	Yes	50	40	60
05.01.20	No	20	10	10
06.01.20	Yes	60	60	70
07.01.20		50	40	50
08.01.20			10	0
09.01.20				10
09.01.20
:

This is how your forecast diary might look like on 6th of Jan, 2020. Here, Probability of Precipitation forecasts (in percent) up to a lead time of three days are recorded in separate columns with headings , and .

Reliability

Focussing on forecasts for a fixed lead time (say three days), a forecast diary can be used to check the reliability of the forecasting system. In the present situation, this means that if the forecast probability is , then it should indeed rain with probability . More precisely, considering all rows in the diary where the relevant forecast was , we should see rain for a fraction of those rows; and this needs to be checked for all values of that can possibly occur. In our case, there are eleven values: .

In general, assume the forecasts take the values . Assume we recorded days in total, and for each let (or , respectively) be the number of days where the forecast was equal to and there was rain (or no rain, respectively). Following our discussion, we expect that

You can plot the left hand side (the observed frequencies) vs the right hand side (the forecast probabilities) and check if you get something close to the diagonal; this is called a reliability diagram. Here’s an example of a reliability diagram, taken from Bröcker and Smith, 2007:

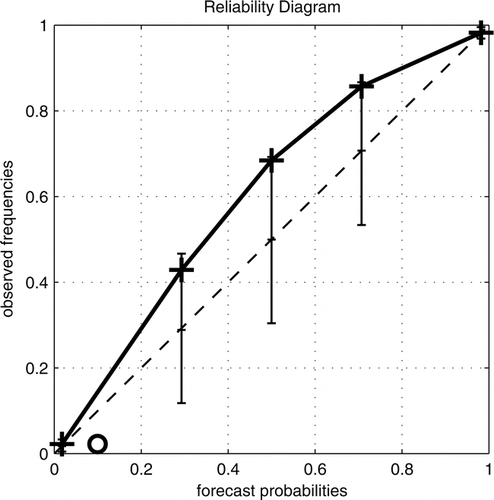
Rearranging the previous equation, we find

Of course, if you compute the left hand side for your forecast diary, due to random fluctuations it won’t equal to zero even if the forecasting system was reliable.
Working out how large these deviations typically are and whether a given deviation is still acceptable is what happens in a statistical test, which is what we will discuss next. For more about reliability diagrams and graphical ways of representing the expected random fluctuations see Bröcker and Smith, 2007.

The central limit theorem

We abbreviate the left hand side of Equation (*) as and realise that if the rows in the diary were stochastically independent, we could apply the central limit theorem and obtain as an immediate consequence that the quantity

would have a -distribution with degrees of freedom (where is the covariance matrix of the ). Note that represents the sum squared deviations we encounter in Equation (*) but in a weighted metric defined by the covariance matrix .

The rows of the diary are not independent though. In fact the whole point of weather forecasting is that the weather today tells us something about the weather tomorrow. Fortunately, this does not preclude the use of the statistical methodology outlined above. The central limit theorem is still applicable provided the correlations between the relevant terms in the sum decay fast enough. That this is indeed the case is shown in Bröcker, 2018 (in a slightly different situation, but the basic idea carries over).

This decay is not due to any (assumed) decay in the temporal correlations of the weather due to chaotic dynamics but follows from the assumption that the forecasts are reliable. Remember, we want to know if the deviations in Equation (*) are large provided the forecasts are reliable; if they are, the assumption of
reliability is untenable.

It needs mentioning though that the covariance matrix is not what you would get if the rows in your diary were independent. This matrix has to be estimated from the data. How to do this is beyond this article but python code implementing the methodology can be found here. Look at the comments in rainscript.py and apply it to raindataL2.csv or, of course, your own forecast diary.

References

Jochen Bröcker.
Assessing the reliability of ensemble forecasting systems under serial dependence.
Quarterly Journal of the Royal Meteorological Society, 144(717), 2018. https://doi.org/10.1002/qj.3379

Jochen Bröcker and Leonard A. Smith.
Increasing the reliability of reliability diagrams.
Weather and Forecasting, 22(3):651–661, June 2007.https://doi.org/10.1175/WAF993.1